Introduccion a los sistemas de computo UMG
Esta información te ayudara a entender mejor los conceptos básicos acerca del curso de Introducción a los sistemas de computo de la Universidad Mariano Gálvez de Guatemala, ya que toda la información que se maneja en este blog es con el fin de ayudar a los estudiantes o cualquier otro tipo de persona para poder adentrarse en la rama de la informática.
miércoles, 27 de julio de 2011
viernes, 22 de julio de 2011
Tarea 1
Tarea No. 1 Ingeniería en Sistemas sección A.
Gutiérrez Casasola Ronald Mauricio Carne: 5190-04-2404
Algoritmos:
1) Inicio
Acción 1
- Poner el sartén al fuego
Acción 2
- Colocar Mantequilla, o aceite
Acción 3
- Poner el huevo a coser y revolver
Acción 4
- Colocar en un plato y listo.
Fin
-------------------------------------------------------------------------------------------------------------------
2) Inicio
Acción 1
- Marcar el numero
Acción 2
- Si es extranjero marcar la clave lada seguido del número telefónico
Acción 3
- Proseguir con la llamada
Fin
-------------------------------------------------------------------------------------------------------------------
3) Inicio
Acción 1
- Var:
- A, B, C.
- Variante A : Multiplicado entero
- Variante B: Multiplicador
- Variante C: Resultado
Ejemplo: 32*5= 160 entonces Multiplicado (variante a) 5 veces seria 32, 5 veces que da un total de 160.
Fin
----------------------------------------------------------------------------------------------------------------------------------
4) Inicio
Acción 1
Variantes X= Numero Entero
Variante Y= Numero entero
Variante Z= Resultado
X, Y, Z son variantes
Acción 2
- X * Y = Z
- Multiplicando las dos variantes nos da como resultado una multiplicación normal
Si x es multiplicado por y entonces el resultado es Z
Fin
-----------------------------------------------------------------------------------------------------------------------------------
5) Inicio
Acción 1
- Ingresar la tarjeta
Acción 2
- Ingresar clave de la tarjeta
Acción 3
- Variantes
- A: Retiro Ahorro
- B: Monetario
- C: Consulta de Saldo
- D: Imprimir
- E: Salir
Acción 3
- Ejecutar la acción deseada
Fin
-------------------------------------------------------------------------------------------------------------------
lunes, 18 de julio de 2011
Análisis de Algoritmos: Complejidad
La resolución práctica de un problema exige por una parte un algoritmo o método de resolución y por otra un programa o codificación de aquel en un ordenador real. Ambos componentes tienen su importancia; pero la del algoritmo es absolutamente esencial, mientras que la codificación puede muchas veces pasar a nivel de anécdota.
A efectos prácticos o ingenieriles, nos deben preocupar los recursos físicos necesarios para que un programa se ejecute. Aunque puede haber muchos parametros, los mas usuales son el tiempo de ejecución y la cantidad de memoria (espacio). Ocurre con frecuencia que ambos parametros están fijados por otras razones y se plantea la pregunta inversa: ¿cual es el tamano del mayor problema que puedo resolver en T segundos y/o con M bytes de memoria? En lo que sigue nos centraremos casi siempre en el parametro tiempo de ejecución, si bien las ideas desarrolladas son fácilmente aplicables a otro tipo de recursos.
Para cada problema determinaremos un medida N de su tamaño (por número de datos) e intentaremos hallar respuestas en función de dicho N. El concepto exacto que mide N depende de la naturaleza del problema. Así, para un vector se suele utizar como N su longitud; para una matriz, el número de elementos que la componen; para un grafo, puede ser el número de nodos (a veces es mas importante considerar el número de arcos, dependiendo del tipo de problema a resolver); en un fichero se suele usar el número de registros, etc. Es imposible dar una regla general, pues cada problema tiene su propia lógica de coste. Una medida que suele ser útil conocer es el tiempo de ejecución de un programa en función de N, lo que denominaremos T(N). Esta función se puede medir físicamente (ejecutando el programa, reloj en mano), o calcularse sobre el código contando instrucciones a ejecutar y multiplicando por el tiempo requerido por cada instrucción. Así, un trozo sencillo de programa como
Prácticamente todos los programas reales incluyen alguna sentencia condicional, haciendo que las sentencias efectivamente ejecutadas dependan de los datos concretos que se le presenten. Esto hace que mas que un valor T(N) debamos hablar de un rango de valores
Cualquier fórmula T(N) incluye referencias al parámetro N y a una serie de constantes "Ti" que dependen de factores externos al algoritmo como pueden ser la calidad del código generado por el compilador y la velocidad de ejecución de instrucciones del ordenador que lo ejecuta. Dado que es fácil cambiar de compilador y que la potencia de los ordenadores crece a un ritmo vertiginoso (en la actualidad, se duplica anualmente), intentaremos analizar los algoritmos con algun nivel de independencia de estos factores; es decir, buscaremos estimaciones generales ampliamente válidas. Por una parte necesitamos analizar la potencia de los algoritmos independientemente de la potencia de la máquina que los ejecute e incluso de la habilidad del programador que los codifique. Por otra, este análisis nos interesa especialmente cuando el algoritmo se aplica a problema grandes. Casi siempre los problemas pequeños se pueden resolver de cualquier forma, apareciendo las limitaciones al atacar problemas grandes. No debe olvidarse que cualquier técnica de ingeniería, si funciona, acaba aplicándose al problema más grande que sea posible: las tecnologias de éxito, antes o después, acaban llevándose al límite de sus posibilidades.
Las consideraciones anteriores nos llevan a estudiar el comportamiento de un algoritmo cuando se fuerza el tamaño del problema al que se aplica. Matemáticamente hablando, cuando N tiende a infinito. Es decir, su comportamiento asintótico.
Sean "g(n)" diferentes funciones que determinan el uso de recursos. Habra funciones "g" de todos los colores. Lo que vamos a intentar es identificar "familias" de funciones, usando como criterio de agrupación su comportamiento asintótico.
A un conjunto de funciones que comparten un mismo comportamiento asintótico le denominaremos un órden de complejidad'. Habitualmente estos conjuntos se denominan O, existiendo una infinidad de ellos.
Para cada uno de estos conjuntos se suele identificar un miembro f(n) que se utiliza como representante de la clase, hablándose del conjunto de funciones "g" que son del orden de "f(n)", denotándose como
La definición matemática de estos conjuntos debe ser muy cuidadosa para involucrar ambos aspectos: identificación de una familia y posible utilización como cota superior de otras funciones menos malas:
De las funciones "g" que forman este conjunto O(f(n)) se dice que "están dominadas asintóticamente" por "f", en el sentido de que para N suficientemente grande, y salvo una constante multiplicativa "k", f(n) es una cota superior de g(n).
Sea un problema que sabemos resolver con algoritmos de diferentes complejidades. Para compararlos entre si, supongamos que todos ellos requieren 1 hora de ordenador para resolver un problema de tamaño N=100.
¿Qué ocurre si disponemos del doble de tiempo? Notese que esto es lo mismo que disponer del mismo tiempo en un odenador el doble de potente, y que el ritmo actual de progreso del hardware es exactamente ese:
Los algoritmos de complejidad logarítmica son un descubrimiento fenomenal, pues en el doble de tiempo permiten atacar problemas notablemente mayores, y para resolver un problema el doble de grande sólo hace falta un poco más de tiempo (ni mucho menos el doble).
Los algoritmos de tipo polinómico no son una maravilla, y se enfrentan con dificultad a problemas de tamaño creciente. La práctica viene a decirnos que son el límite de lo "tratable".
Sobre la tratabilidad de los algoritmos de complejidad polinómica habria mucho que hablar, y a veces semejante calificativo es puro eufemismo. Mientras complejidades del orden O(n2) y O(n3) suelen ser efectivamente abordables, prácticamente nadie acepta algoritmos de orden O(n100), por muy polinómicos que sean. La frontera es imprecisa.
Cualquier algoritmo por encima de una complejidad polinómica se dice "intratable" y sólo será aplicable a problemas ridiculamente pequeños.
A la vista de lo anterior se comprende que los programadores busquen algoritmos de complejidad lineal. Es un golpe de suerte encontrar algo de complejidad logarítmica. Si se encuentran soluciones polinomiales, se puede vivir con ellas; pero ante soluciones de complejidad exponencial, más vale seguir buscando.
No obstante lo anterior ...
Para simplificar la notación, usaremos O(f) para decir O(f(n))
Las primeras reglas sólo expresan matemáticamente el concepto de jerarquía de órdenes de complejidad:
A. La relación de orden definida por
Las siguientes propiedades se pueden utilizar como reglas para el cálculo de órdenes de complejidad. Toda la maquinaria matemática para el cálculo de límites se puede aplicar directamente:
La combinación de las reglas [K, G] es probablemente la más usada, permitiendo de un plumazo olvidar todos los componentes de un polinomio, menos su grado.
Por último, la regla [H] es la basica para analizar el concepto de secuencia en un programa: la composición secuencial de dos trozos de programa es de orden de complejidad el de la suma de sus partes. Aunque no existe una receta que siempre funcione para calcular la complejidad de un algoritmo, si es posible tratar sistematicamente una gran cantidad de ellos, basandonos en que suelen estar bien estructurados y siguen pautas uniformes.
Loa algoritmos bien estructurados combinan las sentencias de alguna de las formas siguientes
El cálculo de la complejidad asociada a un procedimiento puede complicarse notáblemente si se trata de procedimientos recursivos. Es fácil que tengamos que aplicar técnicas propias de la matemática discreta, tema que queda fuera de los límites de esta nota técnica.
Como medida del tamaño tomaremos para N el grado del polinomio, que es el número de coeficientes en C. Así pues, el bucle más exterior (1) se ejecuta N veces. El bucle interior (2) se ejecuta, respectivamente
El análisis de la función Potencia es delicado, pues si el exponente es par, el problema tiene una evolución logarítmica; mientras que si es impar, su evolución es lineal. No obstante, como si "j" es impar entonces "j-1" es par, el caso peor es que en la mitad de los casos tengamos "j" impar y en la otra mitad sea par. El caso mejor, por contra, es que siempre sea "j" par.
Un ejemplo de caso peor seria x31, que implica la siguiente serie para j:
Por tanto, la complejidad de Potencia es de orden O(log n).
Insertada la función Potencia en la función EvaluaPolinomio, la complejidad compuesta es del orden O(n log n), al multiplicarse por N un subalgoritmo de O(log n).
Así y todo, esto sigue resultando estravagante y excesivamente costoso. En efecto, basta reconsiderar el algoritmo almacenando las potencias de "X" ya calculadas para mejorarlo sensiblemente:
que queda en un algoritmo de O(n). Habiendo N coeficientes C distintos, es imposible encontrar ningun algoritmo de un orden inferior de complejidad.
En cambio, si es posible encontrar otros algoritmos de idéntica complejidad:
No obstante ser ambos algoritmos de idéntico orden de complejidad, cabe resaltar que sus tiempos de ejecución serán notablemente distintos. En efecto, mientras el último algoritmo ejecuta N multiplicaciones y N sumas, el penúltimo requiere 2N multiplicaciones y N sumas. Si, como es frecuente, el tiempo de ejecución es notablemente superior para realizar una multiplicación, cabe razonar que el último algoritmo ejecutará en la mitad de tiempo que el anterior.

Estos estudios han llevado a la constatación de que existen problemas muy difíciles, problemas que desafian la utilización de los ordenadores para resolverlos. En lo que sigue esbozaremos las clases de problemas que hoy por hoy se escapan a un tratamiento informático.
En el análisis de algoritmos se considera usualmente el caso peor, si bien a veces conviene analizar igualmente el caso mejor y hacer alguna estimación sobre un caso promedio. Para independizarse de factores coyunturales tales como el lenguaje de programación, la habilidad del codificador, la máquina soporte, etc. se suele trabajar con un cálculo asintótico que indica como se comporta el algoritmo para datos muy grandes y salvo algun coeficiente multiplicativo. Para problemas pequeños es cierto que casi todos los algoritmos son "más o menos iguales", primando otros aspectos como esfuerzo de codificación, legibilidad, etc. Los órdenes de complejidad sólo son importantes para grandes problemas. Es difícil encontrar libros que traten este tema a un nivel introductorio sin caer en amplios desarrollos matemáticos, aunque tambien es cierto que casi todos los libros que se precien dedican alguna breve sección al tema. Probablemente uno de los libros que sólo dedican un capítulo; pero es extremadamente claro es
1. Introducción
A efectos prácticos o ingenieriles, nos deben preocupar los recursos físicos necesarios para que un programa se ejecute. Aunque puede haber muchos parametros, los mas usuales son el tiempo de ejecución y la cantidad de memoria (espacio). Ocurre con frecuencia que ambos parametros están fijados por otras razones y se plantea la pregunta inversa: ¿cual es el tamano del mayor problema que puedo resolver en T segundos y/o con M bytes de memoria? En lo que sigue nos centraremos casi siempre en el parametro tiempo de ejecución, si bien las ideas desarrolladas son fácilmente aplicables a otro tipo de recursos.
Para cada problema determinaremos un medida N de su tamaño (por número de datos) e intentaremos hallar respuestas en función de dicho N. El concepto exacto que mide N depende de la naturaleza del problema. Así, para un vector se suele utizar como N su longitud; para una matriz, el número de elementos que la componen; para un grafo, puede ser el número de nodos (a veces es mas importante considerar el número de arcos, dependiendo del tipo de problema a resolver); en un fichero se suele usar el número de registros, etc. Es imposible dar una regla general, pues cada problema tiene su propia lógica de coste. Una medida que suele ser útil conocer es el tiempo de ejecución de un programa en función de N, lo que denominaremos T(N). Esta función se puede medir físicamente (ejecutando el programa, reloj en mano), o calcularse sobre el código contando instrucciones a ejecutar y multiplicando por el tiempo requerido por cada instrucción. Así, un trozo sencillo de programa como
2. Tiempo de Ejecución
S1; for (int i= 0; i < N; i++) S2;requiere
T(N)= t1 + t2*Nsiendo t1 el tiempo que lleve ejecutar la serie "S1" de sentencias, y t2 el que lleve la serie "S2".
Prácticamente todos los programas reales incluyen alguna sentencia condicional, haciendo que las sentencias efectivamente ejecutadas dependan de los datos concretos que se le presenten. Esto hace que mas que un valor T(N) debamos hablar de un rango de valores
Tmin(N) <= T(N) <= Tmax(N)los extremos son habitualmente conocidos como "caso peor" y "caso mejor". Entre ambos se hallara algun "caso promedio" o más frecuente.
Cualquier fórmula T(N) incluye referencias al parámetro N y a una serie de constantes "Ti" que dependen de factores externos al algoritmo como pueden ser la calidad del código generado por el compilador y la velocidad de ejecución de instrucciones del ordenador que lo ejecuta. Dado que es fácil cambiar de compilador y que la potencia de los ordenadores crece a un ritmo vertiginoso (en la actualidad, se duplica anualmente), intentaremos analizar los algoritmos con algun nivel de independencia de estos factores; es decir, buscaremos estimaciones generales ampliamente válidas. Por una parte necesitamos analizar la potencia de los algoritmos independientemente de la potencia de la máquina que los ejecute e incluso de la habilidad del programador que los codifique. Por otra, este análisis nos interesa especialmente cuando el algoritmo se aplica a problema grandes. Casi siempre los problemas pequeños se pueden resolver de cualquier forma, apareciendo las limitaciones al atacar problemas grandes. No debe olvidarse que cualquier técnica de ingeniería, si funciona, acaba aplicándose al problema más grande que sea posible: las tecnologias de éxito, antes o después, acaban llevándose al límite de sus posibilidades.
3. Asintotas
Las consideraciones anteriores nos llevan a estudiar el comportamiento de un algoritmo cuando se fuerza el tamaño del problema al que se aplica. Matemáticamente hablando, cuando N tiende a infinito. Es decir, su comportamiento asintótico.
Sean "g(n)" diferentes funciones que determinan el uso de recursos. Habra funciones "g" de todos los colores. Lo que vamos a intentar es identificar "familias" de funciones, usando como criterio de agrupación su comportamiento asintótico.
A un conjunto de funciones que comparten un mismo comportamiento asintótico le denominaremos un órden de complejidad'. Habitualmente estos conjuntos se denominan O, existiendo una infinidad de ellos.
Para cada uno de estos conjuntos se suele identificar un miembro f(n) que se utiliza como representante de la clase, hablándose del conjunto de funciones "g" que son del orden de "f(n)", denotándose como
g IN O(f(n))Con frecuencia nos encontraremos con que no es necesario conocer el comportamiento exacto, sino que basta conocer una cota superior, es decir, alguna función que se comporte "aún peor".
La definición matemática de estos conjuntos debe ser muy cuidadosa para involucrar ambos aspectos: identificación de una familia y posible utilización como cota superior de otras funciones menos malas:
Dícese que el conjunto O(f(n)) es el de las funciones de orden de f(n), que se define como O(f(n))= {g: INTEGER -> REAL+ tales que
existen las constantes k y N0 tales que
para todo N > N0, g(N) <= k*f(N) }
en palabras, O(f(n)) esta formado por aquellas funciones g(n) que crecen a un ritmo menor o igual que el de f(n). De las funciones "g" que forman este conjunto O(f(n)) se dice que "están dominadas asintóticamente" por "f", en el sentido de que para N suficientemente grande, y salvo una constante multiplicativa "k", f(n) es una cota superior de g(n).
3.1. Órdenes de Complejidad
Se dice que O(f(n)) define un "orden de complejidad". Escogeremos como representante de este orden a la función f(n) más sencilla del mismo. Así tendremosEs más, se puede identificar una jerarquía de órdenes de complejidad que coincide con el orden de la tabla anterior; jerarquía en el sentido de que cada orden de complejidad superior tiene a los inferiores como subconjuntos. Si un algoritmo A se puede demostrar de un cierto orden O1, es cierto que tambien pertenece a todos los órdenes superiores (la relación de orden çota superior de' es transitiva); pero en la práctica lo útil es encontrar la "menor cota superior", es decir el menor orden de complejidad que lo cubra.
O(1) orden constante O(log n) orden logarítmico O(n) orden lineal O(n log n) O(n2) orden cuadrático O(na) orden polinomial (a > 2) O(an) orden exponencial (a > 2) O(n!) orden factorial
3.1.1. Impacto Práctico
Para captar la importancia relativa de los órdenes de complejidad conviene echar algunas cuentas.Sea un problema que sabemos resolver con algoritmos de diferentes complejidades. Para compararlos entre si, supongamos que todos ellos requieren 1 hora de ordenador para resolver un problema de tamaño N=100.
¿Qué ocurre si disponemos del doble de tiempo? Notese que esto es lo mismo que disponer del mismo tiempo en un odenador el doble de potente, y que el ritmo actual de progreso del hardware es exactamente ese:
"duplicación anual del número de instrucciones por segundo".¿Qué ocurre si queremos resolver un problema de tamaño 2n?
Los algoritmos de complejidad O(n) y O(n log n) son los que muestran un comportamiento más "natural": prácticamente a doble de tiempo, doble de datos procesables.
O(f(n)) N=100 t=2h N=200 log n 1 h 10000 1.15 h n 1 h 200 2 h n log n 1 h 199 2.30 h n2 1 h 141 4 h n3 1 h 126 8 h 2n 1 h 101 1030 h
Los algoritmos de complejidad logarítmica son un descubrimiento fenomenal, pues en el doble de tiempo permiten atacar problemas notablemente mayores, y para resolver un problema el doble de grande sólo hace falta un poco más de tiempo (ni mucho menos el doble).
Los algoritmos de tipo polinómico no son una maravilla, y se enfrentan con dificultad a problemas de tamaño creciente. La práctica viene a decirnos que son el límite de lo "tratable".
Sobre la tratabilidad de los algoritmos de complejidad polinómica habria mucho que hablar, y a veces semejante calificativo es puro eufemismo. Mientras complejidades del orden O(n2) y O(n3) suelen ser efectivamente abordables, prácticamente nadie acepta algoritmos de orden O(n100), por muy polinómicos que sean. La frontera es imprecisa.
Cualquier algoritmo por encima de una complejidad polinómica se dice "intratable" y sólo será aplicable a problemas ridiculamente pequeños.
A la vista de lo anterior se comprende que los programadores busquen algoritmos de complejidad lineal. Es un golpe de suerte encontrar algo de complejidad logarítmica. Si se encuentran soluciones polinomiales, se puede vivir con ellas; pero ante soluciones de complejidad exponencial, más vale seguir buscando.
No obstante lo anterior ...
- ... si un programa se va a ejecutar muy pocas veces, los costes de codificación y depuración son los que más importan, relegando la complejidad a un papel secundario.
- ... si a un programa se le prevé larga vida, hay que pensar que le tocará mantenerlo a otra persona y, por tanto, conviene tener en cuenta su legibilidad, incluso a costa de la complejidad de los algoritmos empleados.
- ... si podemos garantizar que un programa sólo va a trabajar sobre datos pequeños (valores bajos de N), el orden de complejidad del algoritmo que usemos suele ser irrelevante, pudiendo llegar a ser incluso contraproducente. Por ejemplo, si disponemos de dos algoritmos para el mismo problema, con tiempos de ejecución respectivos:
asintóticamente, "f" es mejor algoritmo que "g"; pero esto es cierto a partir de N > 100.algoritmo tiempo complejidad f 100 n O(n) g n2 O(n2)
Si nuestro problema no va a tratar jamás problemas de tamaño mayor que 100, es mejor solución usar el algoritmo "g". El ejemplo anterior muestra que las constantes que aparecen en las fórmulas para T(n), y que desaparecen al calcular las funciones de complejidad, pueden ser decisivas desde el punto de vista de ingeniería. Pueden darse incluso ejemplos más dramaticos:
aún siendo dos algoritmos con idéntico comportamiento asintótico, es obvio que el algoritmo "f" es siempre 100 veces más rápido que el "g" y candidato primero a ser utilizado.algoritmo tiempo complejidad f n O(n) g 100 n O(n) - ... usualmente un programa de baja complejidad en cuanto a tiempo de ejecución, suele conllevar un alto consumo de memoria; y viceversa. A veces hay que sopesar ambos factores, quedándonos en algún punto de compromiso.
- ... en problemas de cálculo numérico hay que tener en cuenta más factores que su complejidad pura y dura, o incluso que su tiempo de ejecución: queda por considerar la precisión del cálculo, el máximo error introducido en cálculos intermedios, la estabilidad del algoritmo, etc. etc.
3.2. Propiedades de los Conjuntos O(f)
No entraremos en muchas profundidades, ni en demostraciones, que se pueden hallar en los libros especializados. No obstante, algo hay que saber de cómo se trabaja con los conjuntos O() para poder evaluar los algoritmos con los que nos encontremos.Para simplificar la notación, usaremos O(f) para decir O(f(n))
Las primeras reglas sólo expresan matemáticamente el concepto de jerarquía de órdenes de complejidad:
A. La relación de orden definida por
f < g <=> f(n) IN O(g)B. f IN O(g) y g IN O(f) <=> O(f) = O(g)
es reflexiva: f(n) IN O(f)
y transitiva: f(n) IN O(g) y g(n) IN O(h) => f(n) IN O(h)
Las siguientes propiedades se pueden utilizar como reglas para el cálculo de órdenes de complejidad. Toda la maquinaria matemática para el cálculo de límites se puede aplicar directamente:
C. Lim(n->inf)f(n)/g(n) = 0 => f IN O(g)
=> g NOT_IN O(f)
=> O(f) es subconjunto de O(g)
D. Lim(n->inf)f(n)/g(n) = k => f IN O(g)
=> g IN O(f)
=> O(f) = O(g)
E. Lim(n->inf)f(n)/g(n)= INF => f NOT_IN O(g)
=> g IN O(f)
=> O(f) es superconjunto de O(g)
Las que siguen son reglas habituales en el cálculo de límites: F. Si f, g IN O(h) => f+g IN O(h)
G. Sea k una constante, f(n) IN O(g) => k*f(n) IN O(g)
H. Si f IN O(h1) y g IN O(h2) => f+g IN O(h1+h2)
I. Si f IN O(h1) y g IN O(h2) => f*g IN O(h1*h2)
J. Sean los reales 0 < a < b => O(na) es subconjunto de O(nb)
K. Sea P(n) un polinomio de grado k => P(n) IN O(nk)
L. Sean los reales a, b > 1 => O(loga) = O(logb)La regla [L] nos permite olvidar la base en la que se calculan los logaritmos en expresiones de complejidad.
La combinación de las reglas [K, G] es probablemente la más usada, permitiendo de un plumazo olvidar todos los componentes de un polinomio, menos su grado.
Por último, la regla [H] es la basica para analizar el concepto de secuencia en un programa: la composición secuencial de dos trozos de programa es de orden de complejidad el de la suma de sus partes. Aunque no existe una receta que siempre funcione para calcular la complejidad de un algoritmo, si es posible tratar sistematicamente una gran cantidad de ellos, basandonos en que suelen estar bien estructurados y siguen pautas uniformes.
4. Reglas Prácticas
Loa algoritmos bien estructurados combinan las sentencias de alguna de las formas siguientes
- sentencias sencillas
- secuencia (;)
- decisión (if)
- bucles
- llamadas a procedimientos
4.0. Sentencias sencillas
Nos referimos a las sentencias de asignación, entrada/salida, etc. siempre y cuando no trabajen sobre variables estructuradas cuyo tamaño este relacionado con el tamaño N del problema. La inmensa mayoría de las sentencias de un algoritmo requieren un tiempo constante de ejecución, siendo su complejidad O(1).4.1. Secuencia (;)
La complejidad de una serie de elementos de un programa es del orden de la suma de las complejidades individuales, aplicándose las operaciones arriba expuestas.4.2. Decisión (if)
La condición suele ser de O(1), complejidad a sumar con la peor posible, bien en la rama THEN, o bien en la rama ELSE. En decisiones multiples (ELSE IF, SWITCH CASE), se tomara la peor de las ramas.4.3. Bucles
En los bucles con contador explícito, podemos distinguir dos casos, que el tamaño N forme parte de los límites o que no. Si el bucle se realiza un número fijo de veces, independiente de N, entonces la repetición sólo introduce una constante multiplicativa que puede absorberse.Ej.- for (int i= 0; i < K; i++) { algo_de_O(1) } => K*O(1) = O(1)
Si el tamaño N aparece como límite de iteraciones ... Ej.- for (int i= 0; i < N; i++) { algo_de_O(1) } => N * O(1) = O(n)
Ej.- for (int i= 0; i < N; i++) {
for (int j= 0; j < N; j++) {
algo_de_O(1)
}
}
tendremos N * N * O(1) = O(n2)
Ej.- for (int i= 0; i < N; i++) {
for (int j= 0; j < i; j++) {
algo_de_O(1)
}
}
el bucle exterior se realiza N veces, mientras que el interior se realiza 1, 2, 3, ... N veces respectivamente. En total, 1 + 2 + 3 + ... + N = N*(1+N)/2 -> O(n2)
A veces aparecen bucles multiplicativos, donde la evolución de la variable de control no es lineal (como en los casos anteriores) Ej.- c= 1;
while (c < N) {
algo_de_O(1)
c= 2*c;
}
El valor incial de "c" es 1, siendo "2k" al cabo de "k" iteraciones. El número de iteraciones es tal que
2k >= N => k= eis (log2 (N)) [el entero inmediato superior]
y, por tanto, la complejidad del bucle es O(log n).
Ej.- c= N;
while (c > 1) {
algo_de_O(1)
c= c / 2;
}
Un razonamiento análogo nos lleva a log2(N) iteraciones y, por tanto, a un orden O(log n) de complejidad.
Ej.- for (int i= 0; i < N; i++) {
c= i;
while (c > 0) {
algo_de_O(1)
c= c/2;
}
}
tenemos un bucle interno de orden O(log n) que se ejecuta N veces, luego el conjunto es de orden O(n log n)
4.4. Llamadas a procedimientos
La complejidad de llamar a un procedimiento viene dada por la complejidad del contenido del procedimiento en sí. El coste de llamar no es sino una constante que podemos obviar inmediatamente dentro de nuestros análisis asintóticos.El cálculo de la complejidad asociada a un procedimiento puede complicarse notáblemente si se trata de procedimientos recursivos. Es fácil que tengamos que aplicar técnicas propias de la matemática discreta, tema que queda fuera de los límites de esta nota técnica.
4.5. Ejemplo: evaluación de un polinomio
Vamos a aplicar lo explicado hasta ahora a un problema de fácil especificación: diseñar un programa para evaluar un polinomio P(x) de grado N;class Polinomio {
private double[] coeficientes;
Polinomio (double[] coeficientes) {
this.coeficientes= new double[coeficientes.length];
System.arraycopy(coeficientes, 0, this.coeficientes, 0,
coeficientes.length);
}
double evalua_1 (double x) {
double resultado= 0.0;
for (int termino= 0; termino < coeficientes.length; termino++) {
double xn= 1.0;
for (int j= 0; j < termino; j++)
xn*= x; // x elevado a n
resultado+= coeficientes[termino] * xn;
}
return resultado;
}
}
|
1 + 2 + 3 + ... + N veces = N*(1+N)/2 => O(n2)Intuitivamente, sin embargo, este problema debería ser menos complejo, pues repugna al sentido común que sea de una complejidad tan elevada. Se puede ser más inteligente a la hora de evaluar la potencia xn:
double evalua_2 (double x) {
double resultado= 0.0;
for (int termino= 0; termino < coeficientes.length; termino++) {
resultado+= coeficientes[termino] * potencia(x, termino);
}
return resultado;
}
private double potencia (double x, int n) {
if (n == 0)
return 1.0;
// si es potencia impar ...
if (n%2 == 1)
return x * potencia(x, n-1);
// si es potencia par ...
double t= potencia(x, n/2);
return t*t;
}
|
Un ejemplo de caso peor seria x31, que implica la siguiente serie para j:
31 30 15 14 7 6 3 2 1cuyo número de terminos podemos acotar superiormente por
2 * eis (log2(j)),donde eis(r) es el entero inmediatamente superior (este cálculo responde al razonamiento de que en el caso mejor visitaremos eis(log2(j)) valores pares de "j"; y en el caso peor podemos encontrarnos con otros tantos números impares entremezclados).
Por tanto, la complejidad de Potencia es de orden O(log n).
Insertada la función Potencia en la función EvaluaPolinomio, la complejidad compuesta es del orden O(n log n), al multiplicarse por N un subalgoritmo de O(log n).
Así y todo, esto sigue resultando estravagante y excesivamente costoso. En efecto, basta reconsiderar el algoritmo almacenando las potencias de "X" ya calculadas para mejorarlo sensiblemente:
double evalua_3 (double x) {
double xn= 1.0;
double resultado= coeficientes[0];
for (int termino= 1; termino < coeficientes.length; termino++) {
xn*= x;
resultado+= coeficientes[termino] * xn;
}
return resultado;
}
|
En cambio, si es posible encontrar otros algoritmos de idéntica complejidad:
double evalua_4 (double x) {
double resultado= 0.0;
for (int termino= coeficientes.length-1; termino >= 0; termino--) {
resultado= resultado * x +
coeficientes[termino];
}
return resultado;
}
|
4.5.1. Medidas de laboratorio
La siguiente tabla muestra algunas medidas de la eficacia de nuestros algoritmos sobre una implementación en Java:| grado | evalua_1 | evalua_2 | evalua_3 | evalua_4 |
|---|---|---|---|---|
| 1 | 0 | 10 | 0 | 0 |
| 2 | 10 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 |
| 10 | 0 | 10 | 0 | 0 |
| 20 | 0 | 10 | 0 | 0 |
| 50 | 40 | 20 | 0 | 10 |
| 100 | 130 | 60 | 0 | 0 |
| 200 | 521 | 140 | 0 | 10 |
| 500 | 3175 | 400 | 10 | 10 |
| 1000 | 63632 | 1171 | 872 | 580 |

5. Problemas P, NP y NP-completos
Estos estudios han llevado a la constatación de que existen problemas muy difíciles, problemas que desafian la utilización de los ordenadores para resolverlos. En lo que sigue esbozaremos las clases de problemas que hoy por hoy se escapan a un tratamiento informático.
- Clase P.-
- Los algoritmos de complejidad polinómica se dice que son tratables en el sentido de que suelen ser abordables en la práctica. Los problemas para los que se conocen algoritmos con esta complejidad se dice que forman la clase P. Aquellos problemas para los que la mejor solución que se conoce es de complejidad superior a la polinómica, se dice que son problemas intratables. Seria muy interesante encontrar alguna solución polinómica (o mejor) que permitiera abordarlos.
- Clase NP.-
- Algunos de estos problemas intratables pueden caracterizarse por el curioso hecho de que puede aplicarse un algoritmo polinómico para comprobar si una posible solución es válida o no. Esta característica lleva a un método de resolución no determinista consistente en aplicar heurísticos para obtener soluciones hipotéticas que se van desestimando (o aceptando) a ritmo polinómico. Los problemas de esta clase se denominan NP (la N de no-deterministas y la P de polinómicos).
- Clase NP-completos.-
- Se conoce una amplia variedad de problemas de tipo NP, de los cuales destacan algunos de ellos de extrema complejidad. Gráficamente podemos decir que algunos problemas se hayan en la "frontera externa" de la clase NP. Son problemas NP, y son los peores problemas posibles de clase NP. Estos problemas se caracterizan por ser todos "iguales" en el sentido de que si se descubriera una solución P para alguno de ellos, esta solución sería fácilmente aplicable a todos ellos. Actualmente hay un premio de prestigio equivalente al Nobel reservado para el que descubra semejante solución ... ¡y se duda seriamente de que alguien lo consiga!
- Es más, si se descubriera una solución para los problemas NP-completos, esta sería aplicable a todos los problemas NP y, por tanto, la clase NP desaparecería del mundo científico al carecerse de problemas de ese tipo. Realmente, tras años de búsqueda exhaustiva de dicha solución, es hecho ampliamente aceptado que no debe existir, aunque nadie ha demostrado, todavía, la imposibilidad de su existencia.
6. Conclusiones
En el análisis de algoritmos se considera usualmente el caso peor, si bien a veces conviene analizar igualmente el caso mejor y hacer alguna estimación sobre un caso promedio. Para independizarse de factores coyunturales tales como el lenguaje de programación, la habilidad del codificador, la máquina soporte, etc. se suele trabajar con un cálculo asintótico que indica como se comporta el algoritmo para datos muy grandes y salvo algun coeficiente multiplicativo. Para problemas pequeños es cierto que casi todos los algoritmos son "más o menos iguales", primando otros aspectos como esfuerzo de codificación, legibilidad, etc. Los órdenes de complejidad sólo son importantes para grandes problemas. Es difícil encontrar libros que traten este tema a un nivel introductorio sin caer en amplios desarrollos matemáticos, aunque tambien es cierto que casi todos los libros que se precien dedican alguna breve sección al tema. Probablemente uno de los libros que sólo dedican un capítulo; pero es extremadamente claro es
7. Bibliografia
L. Goldschlager and A. Lister.Siempre hay algún clásico con una presentación excelente, pero entrando en mayores honduras matemáticas como
Computer Science, A Modern Introduction
Series in Computer Science. Prentice-Hall Intl., London (UK), 1982.
A. V. Aho, J. E. Hopcroft, and J. D. Ullman.Recientemente ha aparecido un libro en castellano con una presentación muy buena, si bien esta escrito en plan matemático y, por tanto, repleto de demostraciones (un poco duro)
Data Structures and Algorithms
Addison-Wesley, Massachusetts, 1983.
Carmen TorresPara un estudio serio hay que irse a libros de matemática discreta, lo que es toda una asignatura en sí misma; pero se pueden recomendar un par de libros modernos, prácticos y especialmente claros:
Diseño y Análisis de Algoritmos
Paraninfo, 1992
R. Skvarcius and W. B. Robinson.Para saber más de problemas NP y NP-completos, hay que acudir a la "biblia", que en este tema se denomina
Discrete Mathematics with Computer Science Applications
Benjamin/Cummings, Menlo Park, California, 1986.
R. L. Graham, D. E. Knuth, and O. Patashnik.
Concrete Mathematics
Addison-Wesley, 1990.
M. R. Garey and D. S. Johnson.Sólo a efectos documentales, permítasenos citar al inventor de las nociones de complejidad y de la notación O():
Computers and Intractability: A Guide to the Theory of NP-Completeness
Freeman, 1979.
P. BachmannAntes de realizar un programa conviene elegir un buen algoritmo, donde por bueno entendemos que utilice pocos recursos, siendo usualmente los más importantes el tiempo que lleve ejecutarse y la cantidad de espacio en memoria que requiera. Es engañoso pensar que todos los algoritmos son "más o menos iguales" y confiar en nuestra habilidad como programadores para convertir un mal algoritmo en un producto eficaz. Es asimismo engañoso confiar en la creciente potencia de las máquinas y el abaratamiento de las mismas como remedio de todos los problemas que puedan aparecer. Hasta aquí hemos venido hablando de algoritmos. Cuando nos enfrentamos a un problema concreto, habrá una serie de algoritmos aplicables. Se suele decir que el orden de complejidad de un problema es el del mejor algoritmo que se conozca para resolverlo. Así se clasifican los problemas, y los estudios sobre algoritmos se aplican a la realidad.
Analytische Zahlen Theorie
1894
Ciencias de la computación
Las ciencias de la computación son aquellas que abarcan el estudio de las bases teóricas de la información y la computación, así como su aplicación en sistemas computacionales.[1] [2] [3] Existen diversos campos o disciplinas dentro de las Ciencias de la Computación o Ciencias Computacionales; algunos enfatizan los resultados específicos del cómputo (como los gráficos por computadora), mientras que otros (como la teoría de la complejidad computacional) se relacionan con propiedades de los algoritmos usados al realizar cómputos. Otros por su parte se enfocan en los problemas que requieren la implementación de cómputos. Por ejemplo, los estudios de la teoría de lenguajes de programación describen un cómputo, mientras que la programación de computadoras aplica lenguajes de programación específicos para desarrollar una solución a un problema computacional concreto. La informática se refiere al tratamiento automatizado de la información de una forma útil y oportuna. No se debe confundir el carácter teórico de esta ciencia con otros aspectos prácticos como Internet.
Historia
La historia de la ciencia de la computación antecede a la invención del computador digital moderno. Antes de la década de 1920, el término computador se refería a un ser humano que realizaba cálculos.[5] Los primeros investigadores en lo que después se convertiría las ciencias de la computación, estaban interesados en la cuestión de la computabilidad: qué cosas pueden ser computadas por un ser humano que simplemente siga una lista de instrucciones con lápiz y papel, durante el tiempo que sea necesario, con ingenuidad y sin conocimiento previo del problema. Parte de la motivación para este trabajo era el desarrollar máquinas que computaran, y que pudieran automatizar el tedioso y lleno de errores trabajo de la computación humana.
Durante la década de 1940, conforme se desarrollaban nuevas y más poderosas máquinas para computar, el término computador se comenzó a utilizar para referirse a las máquinas en vez de a sus antecesores humanos. Conforme iba quedando claro que las computadoras podían usarse para más cosas que solamente cálculos matemáticos, el campo de la ciencia de la computación se fue ampliando para estudiar a la computación (informática) en general. La ciencia de la computación comenzó entonces a establecerse como una disciplina académica en la década de 1960, con la creación de los primeros departamentos de ciencia de la computación y los primeros programas de licenciatura (Denning 2000).
Las ciencias de la computación frecuentemente se cruzan con otras áreas de investigación, tales como la física y la lingüística. Pero es con las matemáticas con las que se considera que tiene un grado mayor de relación. Eso es evidenciado por el hecho de que los primeros trabajos en el área fueran fuertemente influenciados por matemáticos como Kurt Gödel y Alan Turing. En la actualidad sigue habiendo un intercambio de ideas útil entre ambos campos en áreas como la lógica matemática, la teoría de categorías, la teoría de dominios, el álgebra y la geometría.
Otro punto a destacar es que a pesar de su nombre, las ciencias de la computación raramente involucran el estudio mismo de las máquinas conocidas como computadoras. De hecho, el renombrado científico Edsger Dijkstra es muy citado por la frase "Las ciencias de la computación están tan poco relacionadas con las computadoras como la astronomía con los telescopios." Debido a esto, se propuso buscar un nombre definido para esta ciencia emergente, que evitara la relación con las computadoras.
Una primera propuesta fue la de Peter Naur, que acuñó el término datología, para reflejar el hecho de que la nueva disciplina se ocupaba fundamentalmente del tratamiento de los datos, independientemente de las herramientas de dicho tratamiento, fueran computadoras o artificios matemáticos. La primera institución científica en adoptar la denominación fue el Departamento de Datología de la Universidad de Copenage, fundado en 1969, siendo el propio Peter Naur el primer profesor de datología. Esta denominación se utiliza principalmente en los países escandinavos. Asimismo, en los primeros momentos, un gran número de términos aparecieron asociados a los practicantes de la computación. En esta lista se pueden ver los sugeridos en las revistas y comunicados de ACM : turingeniero, turologista, hombre de los diagramas de flujo(flow-charts-man), metamatemático aplicado, y epistemólogo aplicado.
Tres meses más tarde se sugirió el término contólogo, seguido de hipólogo al año siguiente. También se sugirió el término compútica para la disciplina. Informática era el término más frecuentemente usado en toda Europa.
El diseño y desarrollo de computadoras y sistemas computacionales está generalmente considerado como un campo reclamado por disciplinas ajenas a las ciencias de la computación. Por ejemplo, el estudio del hardware está usualmente considerado como parte de la ingeniería informática, mientras que el estudio de sistemas computacionales comerciales y su desarrollo es usualmente llamado tecnologías de la información (TI) o sistemas de información. Sin embargo, hay una estrecha comunicación de ideas entre las distintas disciplinas relacionadas con las computadoras. La ciencia de la computación a menudo es criticada desde otros estamentos que la consideran escasamente rigurosa y científica. Esta opinión se plasma en la expresión: "La ciencia es a las ciencias de la computación como la hidrodinámica a la fontanería", atribuida a Stan Kelly-Bootle y otros afines. La investigación en ciencias de la computación usualmente también se relaciona con otras disciplinas, como la ciencia cognitiva, la física (véase computación cuántica), la lingüística, etc.
La relación entre las ciencias de la computación y la ingeniería de software es un tema muy discutido, por disputas sobre lo que realmente significa el término "ingeniería de software" y sobre cómo se define a las ciencias de la computación. Algunas personas creen que la ingeniería de software sería un subconjunto de las ciencias de la computación. Otras por su parte, tomando en cuenta la relación entre otras disciplinas científicas y de la ingeniería, creen que el principal objetivo de las ciencias de la computación sería estudiar las propiedades del cómputo en general, mientras que el objetivo de la ingeniería de software sería diseñar cómputos específicos para lograr objetivos prácticos, con lo que se convertirían en disciplinas diferentes. Este punto de vista es mantenido, entre otros por (Parnas 1998). Incluso hay otros que sostienen que no podría existir una ingeniería de software.
Los aspectos académicos, políticos y de financianción en las áreas de ciencias de la computación tienden a estar drásticamente influenciados por el criterio del departamento encargado de la investigación y la educación en cada universidad, que puede estar orientado a la matemática o a la ingeniería. Los departamentos de ciencias de la computación orientados a la matemática suelen alinearse del lado de la computación científica y las aplicaciones de cálculo numérico.
El término computación científica, que no debe confundirse con ciencia de la computación, designa a todas aquellas prácticas destinadas a modelar, plantear experimentos y validar teorías científicas sirviéndose de medios computacionales. En estos casos la computación es una mera herramienta y el esfuerzo se dirige a avanzar en los campos objetivo (física, biología, mecánica de fluidos, radiotransmisión,...) mas que en la propia ciencia de la computación.
Finalmente, el público en general algunas veces confunde la ciencia de la computación con áreas vocacionales que trabajan con computadoras, o piensan que trata acerca de su propia experiencia con las computadoras, lo cual típicamente envuelve actividades como los juegos, la navegación web, y el procesamiento de texto. Sin embargo, el punto central de la ciencia de la computación va más allá de entender las propiedades de los programas que se emplean para implementar aplicaciones de software como juegos y navegadores web, y utiliza ese entendimiento para crear nuevos programas o mejorar los existentes.
Historia
La historia de la ciencia de la computación antecede a la invención del computador digital moderno. Antes de la década de 1920, el término computador se refería a un ser humano que realizaba cálculos.[5] Los primeros investigadores en lo que después se convertiría las ciencias de la computación, estaban interesados en la cuestión de la computabilidad: qué cosas pueden ser computadas por un ser humano que simplemente siga una lista de instrucciones con lápiz y papel, durante el tiempo que sea necesario, con ingenuidad y sin conocimiento previo del problema. Parte de la motivación para este trabajo era el desarrollar máquinas que computaran, y que pudieran automatizar el tedioso y lleno de errores trabajo de la computación humana.
Durante la década de 1940, conforme se desarrollaban nuevas y más poderosas máquinas para computar, el término computador se comenzó a utilizar para referirse a las máquinas en vez de a sus antecesores humanos. Conforme iba quedando claro que las computadoras podían usarse para más cosas que solamente cálculos matemáticos, el campo de la ciencia de la computación se fue ampliando para estudiar a la computación (informática) en general. La ciencia de la computación comenzó entonces a establecerse como una disciplina académica en la década de 1960, con la creación de los primeros departamentos de ciencia de la computación y los primeros programas de licenciatura (Denning 2000).
Campos de las ciencias de la computación
Fundamentos matemáticos
- Criptografía
- Consta de algoritmos para proteger datos privados, incluyendo el cifrado.
- Teoría de grafos
- Recursos elementales para las estructuras de almacenamiento de datos y para los algoritmos de búsqueda.
- Lógica matemática
- Teoría de tipos
- Análisis formal de los tipos de datos, y el uso de estos para entender las propiedades de los programas, en particular la seguridad de estos.
Teoría de la computación
- Teoría de la computación
- Teoría de autómatas
- Teoría de la computabilidad
- Teoría de la complejidad computacional
- Límites fundamentales (en especial de espacio en memoria y tiempo) de los cómputos.
Algoritmos y estructuras de datos
- Análisis de algoritmos
- Algoritmos
- procesos formales usados para los cómputos, y eficiencia de estos procesos.
- Estructuras de datos
- organización y manipulación de los datos
Lenguajes de programación y compiladores
- Compiladores
- formas de traducir programas computacionales, usualmente a partir de lenguajes de alto nivel a lenguajes de bajo nivel.
- Teoría de lenguajes de programación
- lenguajes formales para expresar algoritmos y las propiedades de estos lenguajes.
Bases de datos
- Minería de datos
- estudio de algoritmos para buscar y procesar información en documentos y bases de datos; muy relacionada con la adquisición de información.
Sistemas concurrentes, paralelos y distribuidos
- Programación concurrente
- teoría y práctica de cómputos simultáneos y computación interactiva.
- Redes de computadoras
- algoritmos y protocolos para comunicar eficientemente datos a través de largas distancias, incluye también la corrección de errores.
- Cómputo paralelo
- computación usando múltiples computadoras y múltiples procesadores en paralelo.
- Sistemas Distribuidos
- sistemas utilizando múltiples procesadores repartidos en una gran área geográfica.
Inteligencia artificial
- Inteligencia artificial
- la implementación y estudio de sistemas que exhiben (ya sea por su comportamiento o aparentemente) una inteligencia autónoma o comportamiento propio, a veces inspirado por las características de los seres vivos. Las ciencias de la computación están relacionadas con la IA, ya que el software y las computadoras son herramientas básicas para el desarrollo y progreso de la inteligencia artificial.
- Razonamiento automatizado
- Robótica
- algoritmos para controlar el comportamiento de los robots.
- Visión por computador
- algoritmos para extraer objetos tridimensionales de una imagen bidimensional.
- Aprendizaje Automático
Gráficos por computador
- Computación gráfica
- algoritmos tanto para generar sintéticamente imágenes visuales como para integrar o alterar la información visual y espacial tomada del mundo real.
- Procesamiento digital de imágenes
- por ejemplo para sensores remotos.
- Geometría Computacional
- por ejemplo algoritmos veloces para seleccionar sólo los puntos visibles en un poliedro visto desde cierto ángulo, usado en motores 3D
Computación científica
- Bioinformática
- Computación Cuántica
- Paradigma de computación basado en la Mecánica Cuántica
Relación con otros campos
Por ser una disciplina reciente, existen varias definiciones alternativas para la ciencia de la computación. Esta puede ser vista como una forma de ciencia, matemáticas o una nueva disciplina que no puede ser categorizada siguiendo los modelos actuales.Las ciencias de la computación frecuentemente se cruzan con otras áreas de investigación, tales como la física y la lingüística. Pero es con las matemáticas con las que se considera que tiene un grado mayor de relación. Eso es evidenciado por el hecho de que los primeros trabajos en el área fueran fuertemente influenciados por matemáticos como Kurt Gödel y Alan Turing. En la actualidad sigue habiendo un intercambio de ideas útil entre ambos campos en áreas como la lógica matemática, la teoría de categorías, la teoría de dominios, el álgebra y la geometría.
Otro punto a destacar es que a pesar de su nombre, las ciencias de la computación raramente involucran el estudio mismo de las máquinas conocidas como computadoras. De hecho, el renombrado científico Edsger Dijkstra es muy citado por la frase "Las ciencias de la computación están tan poco relacionadas con las computadoras como la astronomía con los telescopios." Debido a esto, se propuso buscar un nombre definido para esta ciencia emergente, que evitara la relación con las computadoras.
Una primera propuesta fue la de Peter Naur, que acuñó el término datología, para reflejar el hecho de que la nueva disciplina se ocupaba fundamentalmente del tratamiento de los datos, independientemente de las herramientas de dicho tratamiento, fueran computadoras o artificios matemáticos. La primera institución científica en adoptar la denominación fue el Departamento de Datología de la Universidad de Copenage, fundado en 1969, siendo el propio Peter Naur el primer profesor de datología. Esta denominación se utiliza principalmente en los países escandinavos. Asimismo, en los primeros momentos, un gran número de términos aparecieron asociados a los practicantes de la computación. En esta lista se pueden ver los sugeridos en las revistas y comunicados de ACM : turingeniero, turologista, hombre de los diagramas de flujo(flow-charts-man), metamatemático aplicado, y epistemólogo aplicado.
Tres meses más tarde se sugirió el término contólogo, seguido de hipólogo al año siguiente. También se sugirió el término compútica para la disciplina. Informática era el término más frecuentemente usado en toda Europa.
El diseño y desarrollo de computadoras y sistemas computacionales está generalmente considerado como un campo reclamado por disciplinas ajenas a las ciencias de la computación. Por ejemplo, el estudio del hardware está usualmente considerado como parte de la ingeniería informática, mientras que el estudio de sistemas computacionales comerciales y su desarrollo es usualmente llamado tecnologías de la información (TI) o sistemas de información. Sin embargo, hay una estrecha comunicación de ideas entre las distintas disciplinas relacionadas con las computadoras. La ciencia de la computación a menudo es criticada desde otros estamentos que la consideran escasamente rigurosa y científica. Esta opinión se plasma en la expresión: "La ciencia es a las ciencias de la computación como la hidrodinámica a la fontanería", atribuida a Stan Kelly-Bootle y otros afines. La investigación en ciencias de la computación usualmente también se relaciona con otras disciplinas, como la ciencia cognitiva, la física (véase computación cuántica), la lingüística, etc.
La relación entre las ciencias de la computación y la ingeniería de software es un tema muy discutido, por disputas sobre lo que realmente significa el término "ingeniería de software" y sobre cómo se define a las ciencias de la computación. Algunas personas creen que la ingeniería de software sería un subconjunto de las ciencias de la computación. Otras por su parte, tomando en cuenta la relación entre otras disciplinas científicas y de la ingeniería, creen que el principal objetivo de las ciencias de la computación sería estudiar las propiedades del cómputo en general, mientras que el objetivo de la ingeniería de software sería diseñar cómputos específicos para lograr objetivos prácticos, con lo que se convertirían en disciplinas diferentes. Este punto de vista es mantenido, entre otros por (Parnas 1998). Incluso hay otros que sostienen que no podría existir una ingeniería de software.
Los aspectos académicos, políticos y de financianción en las áreas de ciencias de la computación tienden a estar drásticamente influenciados por el criterio del departamento encargado de la investigación y la educación en cada universidad, que puede estar orientado a la matemática o a la ingeniería. Los departamentos de ciencias de la computación orientados a la matemática suelen alinearse del lado de la computación científica y las aplicaciones de cálculo numérico.
El término computación científica, que no debe confundirse con ciencia de la computación, designa a todas aquellas prácticas destinadas a modelar, plantear experimentos y validar teorías científicas sirviéndose de medios computacionales. En estos casos la computación es una mera herramienta y el esfuerzo se dirige a avanzar en los campos objetivo (física, biología, mecánica de fluidos, radiotransmisión,...) mas que en la propia ciencia de la computación.
Finalmente, el público en general algunas veces confunde la ciencia de la computación con áreas vocacionales que trabajan con computadoras, o piensan que trata acerca de su propia experiencia con las computadoras, lo cual típicamente envuelve actividades como los juegos, la navegación web, y el procesamiento de texto. Sin embargo, el punto central de la ciencia de la computación va más allá de entender las propiedades de los programas que se emplean para implementar aplicaciones de software como juegos y navegadores web, y utiliza ese entendimiento para crear nuevos programas o mejorar los existentes.
¿TIPOS DE ALGORITMOS…?
¿TIPOS DE ALGORITMOS…?
Existen dos tipos y son llamados así por su naturaleza:
Lenguajes Algorítmicos
Un Lenguaje algorítmico es una serie de símbolos y reglas que se utilizan para describir de manera explícita un proceso.
Tipos de Lenguajes Algorítmicos
Existen dos tipos y son llamados así por su naturaleza:
- Cualitativos: Son aquellos en los que se describen los pasos utilizando palabras.
- Cuantitativos: Son aquellos en los que se utilizan cálculos numéricos para definir los pasos del proceso.
Lenguajes Algorítmicos
Un Lenguaje algorítmico es una serie de símbolos y reglas que se utilizan para describir de manera explícita un proceso.
Tipos de Lenguajes Algorítmicos
- Gráficos: Es la representación gráfica de las operaciones que realiza un algoritmo (diagrama de flujo).
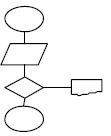
- No Gráficos: Representa en forma descriptiva las operaciones que debe realizar un algoritmo (pseudocodigo).
INICIO
Edad: Entero
ESCRIBA “cual es tu edad?”
Lea Edad
SI Edad >=18 entonces
ESCRIBA “Eres mayor de Edad”
FINSI
ESCRIBA “fin del algoritmo”
FIN
Suscribirse a:
Entradas (Atom)